NeRF2-Neural Radio-Frequency Radiance Fields 笔记

发表于 更新于 分类于 ， Waline： 阅读次数：
NeRF2--MobiCom23--论文机翻笔记

0 简介

Title: NeRF2: Neural Radio-Frequency Radiance Fields: 神经射频辐射场

项目链接: https://xpengzhao.github.io/NeRF2/

该博客说是笔记, 其实是翻译更准确一些. (机翻 仅供个人参考)

ABSTRACT

虽然麦克斯韦早在160年前就发现了电磁波的物理规律，但如何精确地模拟射频信号在电大而复杂的环境中的传播仍然是一个长期存在的问题。

由于射频信号与障碍物之间复杂的相互作用(反射、 衍射等), 如何精确地模拟射频信号在大型而复杂的电气环境中的传播仍然是一个长期存在的问题。

受到NeRF的启发, 本文提出了NeRF2

2 NeRF2 Design

Similar assumptions:(基本假设):

  1. 接受天线(例如: 5G基站, 蓝牙站点或者RFID reader)位置固定, 而发射机(例如，智能手机、iBeacon和RFID标签)可以在有限的范围内移动.
  2. 每个场景中的主要障碍物(例如，建筑物、墙壁和家具)保持不变。
  3. 移动障碍物可能会对辐射场产生暂时的微小扰动，可以通过上层滤波算法(如卡尔曼滤波)对其进行平滑，因此不考虑它们的影响。

Two key components:(两个关键组件):

  1. Neural Radiance Network: 该网络使用两个MLP来表示场景和辐射场。它可以预测射频信号在场景中的分布情况。

  2. Ray Tracing: 在给定射频分布的情况下，我们必须追踪从所有可能的方向发射的信号，以了解接收到的是什么信号。

2.1 Neural Radiance Network

我们将感兴趣的场景离散为空间中有限数量的小3D体素。 惠更斯-菲涅耳原理(Huygens–Fresnel principle)表明，当原始射频信号从所有可能的路径到达它时，体素可以被认为是重新传输该射频信号的新的辐射源。 为了更好地理解这一原理，我们在图1的放大图中显示了一个样例体素。

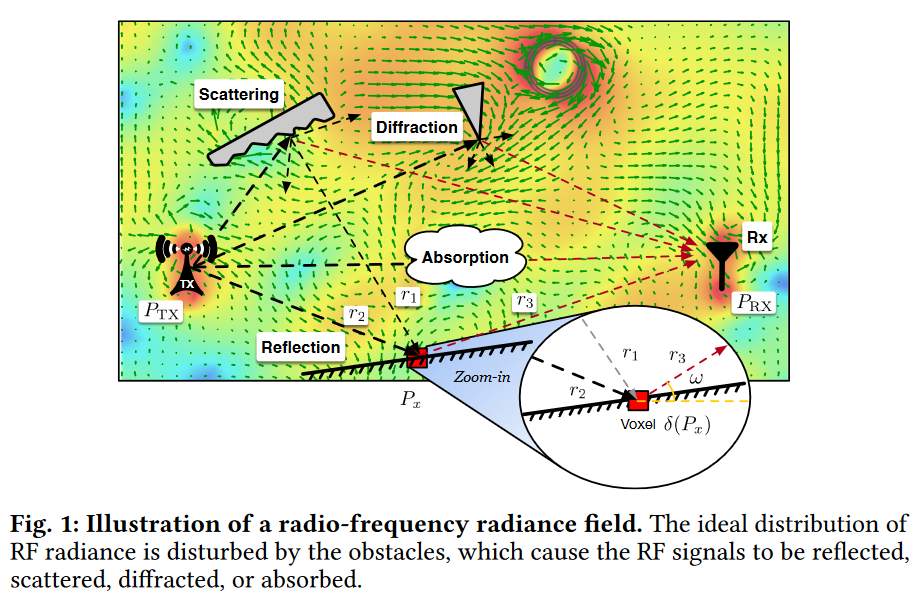
让下标x表示场景中的任意体素。位置Px处的体素x从两个路径R1和R2接收RF信号，并且它成为沿路径R3向Rx重发RF信号的新Tx。

在我们的模型中，每个体素被描述为三个属性，

  1. the position: \(P_x=(X，Y，Z)\)
  2. the attenuation(衰减): \(δ(P_x)=Δa(P_x)E^{jΔθ(P_x)}\)
  3. the retransmitted RF signal(重发的RF信号): \(S(P_x)\)

其中:

  • \(\delta(P_x)\)是一个与材料有关的变量，它表示如果RF信号在\(P_x\)处穿过体素，则幅度降低\(Δa(P_x)=|δ(P_x)|\)，并且相位旋转 \(Δθ(P_x)=\angleδ(P_x)\)。

  • 作为一种新的RX，位置\(P_x\)处的体素重发一个新的复值信号\(S_x\)，即\(S(P_x)=\alpha(P_x)e^{Jθ(P_x)}\)

    • 其中\(θ(P_x)\)和\(\alpha(P_x)\)是初始相位和初始幅度。

体素不能简单地建模为全向辐射源。相反，它可能会以不均匀的角度辐射电磁波。为了解决这个问题，我们引入了另一个变量，称为测量方向\(ω=(α，β)\)，其中\(α\)和\(β\)是方位角和仰角。

如图1的放大图所示，体素位于相对于RX位置的方向ω上.

NeRF2旨在预测在给定Tx的位置\(P_{TX}\)时，从\(P_x\)处的体素向ω方向重新传输的RF信号\(S_x\) 为此，我们利用神经网络对辐射场进行拟合。

形式上，辐射场F表示如下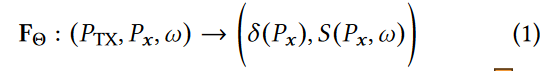： where Θ indicates the learnable neural network weights.

与假设环境光保持不变的可视NERF不同，我们引入TX的位置作为附加输入，因为我们的发射器(例如，智能手机或物联网设备)是可移动的。这样，我们可以通过将TX放置在不同和足够的位置来为场景创建数据集。

输出:

  • 一个是体素在\(P_x\)处的衰减\(δ(P_x)\)，它与体素的物理特性高度相关。

  • 另一个是从\(P_x\)处的体素向ω方向重新传输的RF信号\(S(P_x，ω)\)。

因此，神经网络不仅可以表示场景，还可以表示射频分布。

Network Architecture: 为了建立神经网络，我们采用了两个MLP：衰减网络和辐射网络，如图3所示。

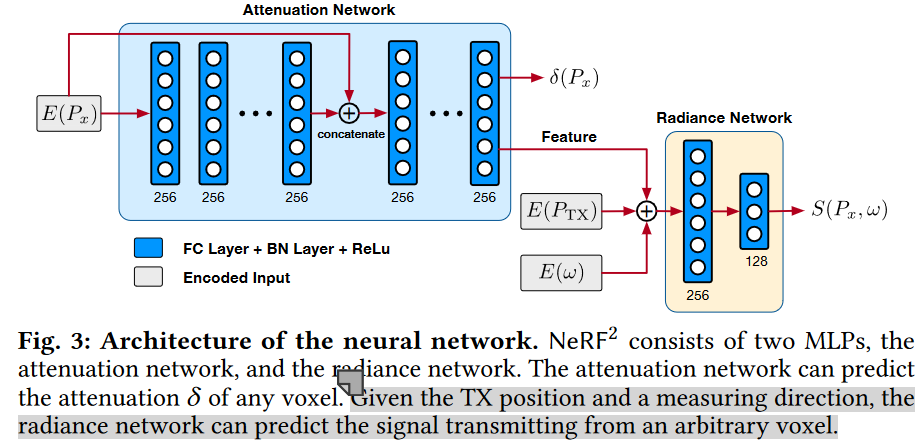
attenuation property(衰减特性)与体素的材料高度相关，与输入信号无关，因此我们分离attenuation network(衰减网络)以预测衰减\(δ(P_x)\)作为位置\(P_x\)的函数。 衰减网络由8个完全连接的层(使用RELU激活和每层256个通道)组成，并输出\(δ(P_x)\)和256维特征向量。

然后，将该特征向量与与\(P_x\)相关的Rx方向\(ω\)和Tx位置\(P_{TX}\)连接。该组合被传递到辐射网络，即另外两个完全连接的层(使用RELU激活并且包括255和128个通道)，其输出方向相关的RF信号\(S(P_x，ω)\)，该信号从体素沿方向ω被重传。

该网络体系结构类似于optical NeRF，但在两个方面有所不同。

  • 首先，视觉神经假设TX(即光源)的位置保持不变，而我们的TX是可移动的。

  • 其次，我们的两个网络都是复值的，既考虑了幅度也考虑了相位。

2.2 Electromagnetic Ray Tracing

为了训练NeRF2, 一种天真的方法是在大量的RX位置探测RF信号。显然，这种方法在实践中是不可扩展的。Visual NeRF将场景的每个图像视为光线行进1的结果，其中每个像素反映由于相机的针孔模型而从特定方向传播的光的强度。 类似地，在RX接收到的信号是电磁射线跟踪的结果，其中信号是从所有可能的方向发射的信号的组合。 接下来，我们介绍如何从特定方向跟踪信号。

RF信号S从发射机(TX)到接收机(RX)的传播符合如下弗里斯方程(Friis equation)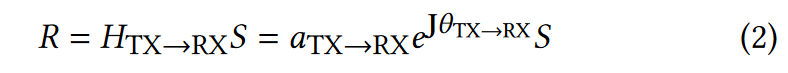： 其中，R是接收信号，\(H_{TX→RX}\)是信道衰减。 特别是，\(\alpha_{TX → RX}\)和\(θ_{TX → RX}\)是由TX到RX的距离引起的幅度退化(amplitude degradation)和相位旋转(phase rotation)。

从数学上讲，可以将与RX相关的方向ω建模为光线，该光线从RX开始并指向ω。该光线上的点相应地描述如下：

其中r是从RX到光线上的点的径向距离。 请注意，\(P_{RX}=P(0，ω)\)。

光线跟踪的目的是累积从该光线上的所有体素发射的RF信号。也就是说，在RX处从方向\(ω\)接收的信号可以表示为：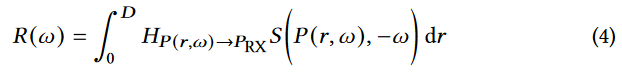

在上面的等式中，\(S(P(r，\omega)，-ω)\)表示从\(P(r，ω)\)处的体素传输到\(P_{RX}\)处的\(RX\)的信号。 它的传输方向与光线的方向相反，所以我们在方程中取ω的负值。 D是穿过场景的最大距离。

上面的等式表明，RX从方向ω接收的最终信号是从射线上的所有体素传输的RF信号的累加，即从\(P(0，ω)\)到\(P(D，ω)\)。

\(H_{P{(r，\omega)}→RX}\)是从点\(P(r，ω)\)传播到Rx的信号的衰减, 它定义如下: 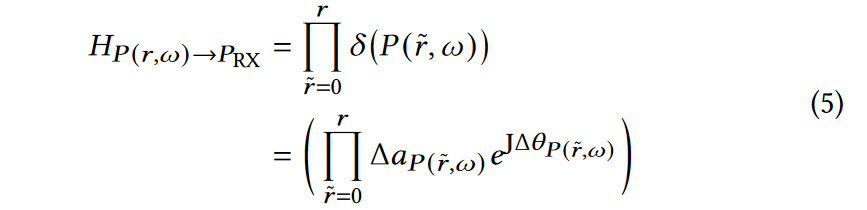上面的公式意味着总衰减等于由\(P(r，\omega)\)和\(P(0, \omega)\)处的体素之间的体素引起的所有衰减的乘积，即\(0 \le \tilde{r} \le r\)。 为了便于计算，我们将上述方程转换为等价的对数标度形式，如下所示：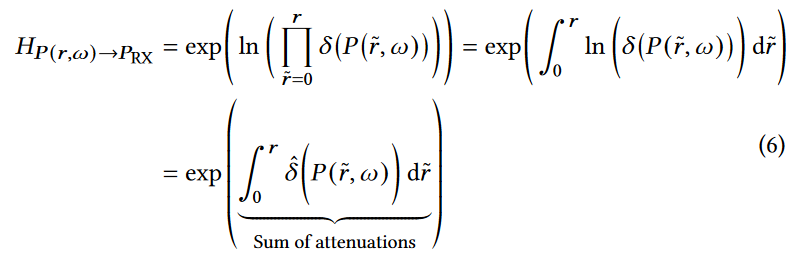

其中\(\hat{δ}(·)\)表示δ(·)的对数衰减，定义如下：

对数尺度的形式使乘积成为两个体素之间所有衰减的和，这极大地方便了计算。代入Equ6->Eqn4，来自ω方向的信号由下式给出:

其中，由衰减网络预测前一部分中涉及的项，并且由辐射网络预测最后部分中涉及的项。

简而言之，光线跟踪的结果是将从该光线上的体素重新传输的信号聚集在一起，每个信号都被视为一个新的源。

同时，来自体素的每个传输必须被当前体素和RX之间的其他体素衰减。假设光线上有N个体素，光线跟踪将采用\(O(N^2)\)个聚集。

为了直观地理解光线跟踪算法，我们在图4中给出了一个例子。 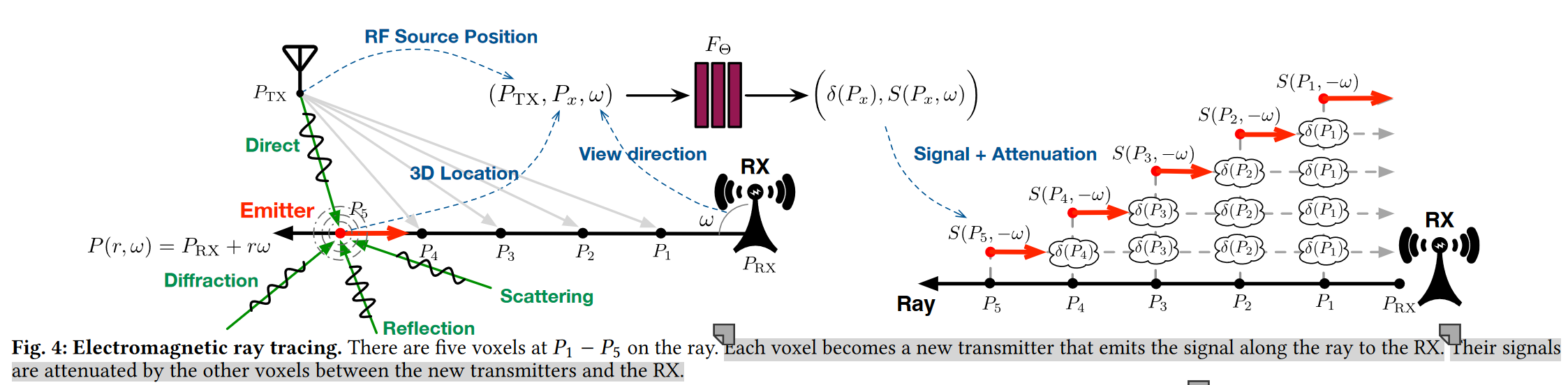假设水平光线从RX向左(i.e. \(\omega = 180°\))。在光线上，在P1、P2、P3、P4和P5处有五个体素, 所有这些都被认为是新的发射器，无论这些体素是如何被照亮的。结果，RX沿着光线的相反方向(即，−ω)接收的信号是从这五个体素重新传输的五个信号的组合。 具体地，从P5处的体素重新发送的信号S5被P4、P3、P2和P1处的体素依次衰减。累积衰减等于\((\hat{δ}_{P1} + \hat{δ}_{P2}+\hat{δ}_{P3}+\hat{δ}_{P4})\)。类似地，从在P1、P2、P3和P4处的体素重发的信号分别被衰减\(0、\hat{δ}_{P1}、\hat{δ}_{P1}+\hat{δ}_{P2}\)和\(\hat{δ}_{P1}+\hat{δ}_{P2}+\hat{δ}_{P3}\)。

Summary: NeRF2并不完全依赖于神经网络，而是将物理模型和统计模型结合起来。 具体地说，射线跟踪采用了众所周知的信号传播物理模型，而深度学习则提供了射频信号与周围障碍物之间复杂相互作用的统计模型。

2.3 Networkd Training

前面描述了光线跟踪算法，通过该算法，我们可以使用NeRF2来预测RX从特定方向接收到的信号。关于在RX上配备哪种类型的天线，我们介绍了两种类型的训练方法。

2.3.1 Case 1: Single-Antenna RX Model.

我们考虑一种简化的情况，其中RX配备了单一的全向或单一定向天线。显然，单个天线在方向上没有辨别能力。因此，RX最终接收的信号是来自所有潜在方向的信号的组合，如下所示：

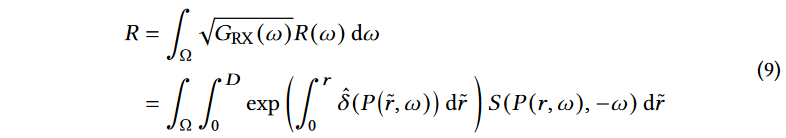
其中\(G_{RX}(ω)\)表示天线的方向性(即，天线在每个方向上提供的增益)，而\(Ω\)表示天线可以覆盖的方向。

设\(R\)和\(\tilde{R}\)分别表示具有光线跟踪的NeRF2预测信号和真实接收信号。

然后，我们可以使用以下损失函数来训练NeRF2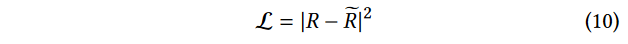： 损失函数的目的是减小真实信号和预测信号之间的差距。

2.3.2 Case 2: Multi-Antenna RX Model

接下来, 我们考虑第二种情况，RX配备了相控阵天线，它可以形成非常窄的波束，并引导它接收来自特定方向的信号. 然后，RX可以区分方向上的信号。 假设天线阵均匀配置\(K×K\)个阵元。选择元素\(A_{1,1}\)作为参考，我们可以计算以下将接收信号投影到ω=(α，β)方向的相对功率：

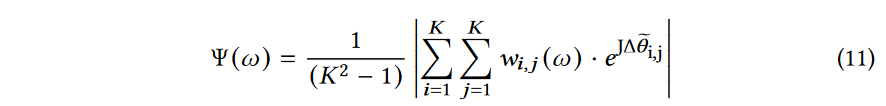
其中\(W_{i，j}(\omega)=e^{J-\Deltaθ_{i，j}}\)是将光束转向某一角度(α，β)所需的复杂weight. 在上面，\(Δ\tilde{θ}_{i,j}\)是通过使用在\(A_{i,j}\)和\(A_{1,1}\)处的接收信号计算的相位差，而\(Δθ\)是它们的理论相位差. 该和聚合了\((K^2−1)\)对元素的相对功率，即\((A_{1, 2}，A_{1,1})、(A_{1, 3},A_{1,1}),···\).当\(Δ\hat{θ}_{i，j}\)与\(Δθ_{i，j}\)对齐时，即信号来自\((α，β)\)方向时，归一化相对功率\(Ψ(α，β)\)应达到最大.

然后可以生成热图以显示接收到的RF信号可能来自的N个可能方向上的相对功率。 我们称这样的2D热图为空间谱，用\(Ψ\)表示。N是取决于角度分辨率的自定义参数。如果接受1度分辨率，则\(N=360×90\)，空间频谱定义如下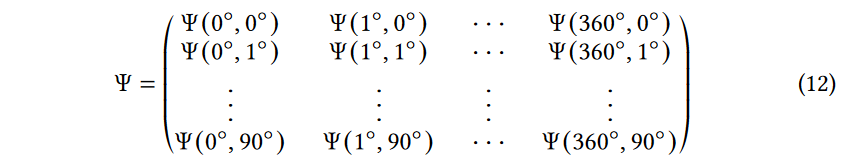： 有时, 空间频谱也称为多径分布，因为它反映了信号是如何从多个方向来的。

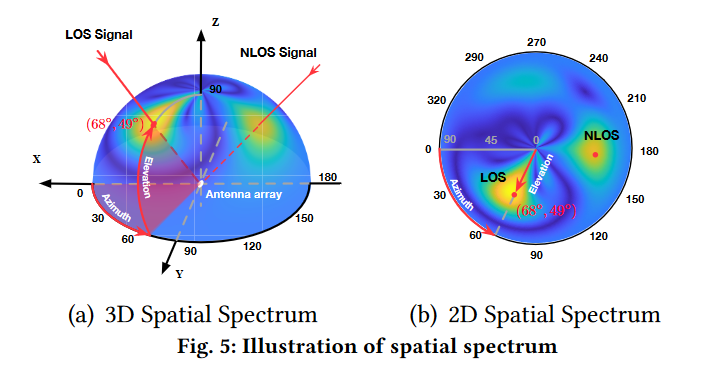图5(a)显示了所有方向均匀分布的3D空间频谱；图5(b)显示了将3D投影到X-Y平面上的2D频谱，其中径向距离表示cos(β)，因此仰角分布不均匀。

NeRF2自发地预测来自特定方向的信号的功率，并生成预测的空间频谱\(Ψ'\)，如下所示：

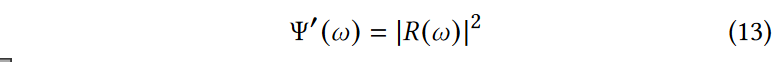
相对功率与上面计算的真实功率成正比。即使它们之间可能存在恒定的偏移量，使用以下损失函数不影响网络的训练：

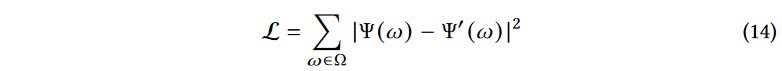
训练的目的是减少从所有可能的方向接收的信号的功率差异。

2.4 Turbo-Learning

作为一种物理层神经网络，NeRF2描述了辐射场的分布。它不能直接满足应用层的需求，如预测接收器的位置或波束形成参数。通常，建立额外的神经网络来满足特定的应用需求(例如，MIMO神经网络、AOA神经网络、定位神经网络等)。相反，我们使用NeRF2作为增强器来提高应用层ANN的性能。

图6说明了这一基本思想。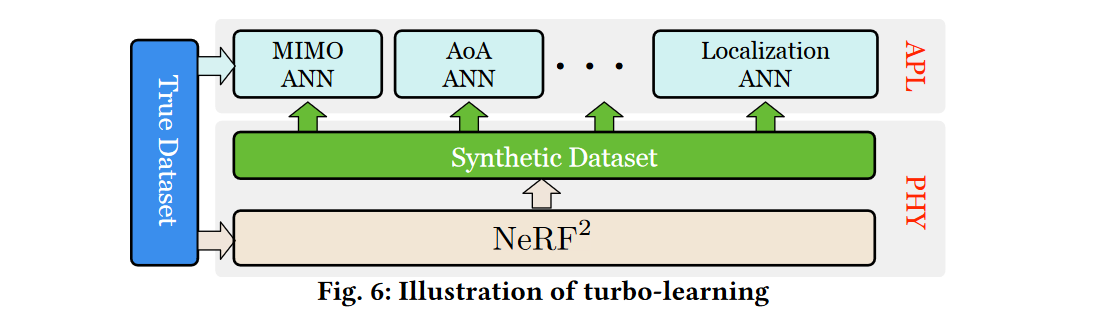

  1. 首先，我们用真实的训练数据集训练NeRF2。
  2. 最后，我们将真实数据集和合成数据集混合在一起来训练上层神经网络。

我们称这种训练方法为Turbo-Learning，即应用更多的额外合成数据来强化学习。 在数据科学领域，Turbo-Learning也被称为数据增强。

3. NeRF2 IMPLEMENTATION

  • 训练NeRF2中的位置信息由OptiTrack提供.

在每次迭代的过程中, 有以下优化:

  1. PositionalEncoding: 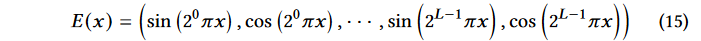对于\(P_{TX}\) 和 \(P_x\) 设置 L = 10, 对于\(\omega\)设置 L = 4;

  2. Voxel Size: 1/8 of the wavelength

  3. Network configuration:

4. MIRCOBENCHMARK

4.1 Experimental Setup

RX: 915MHz 4x4 USRP

TX: The RFID tag is activated by a nearby reader (i.e., 1 m away) and repeatedly transmits RN16 replies.

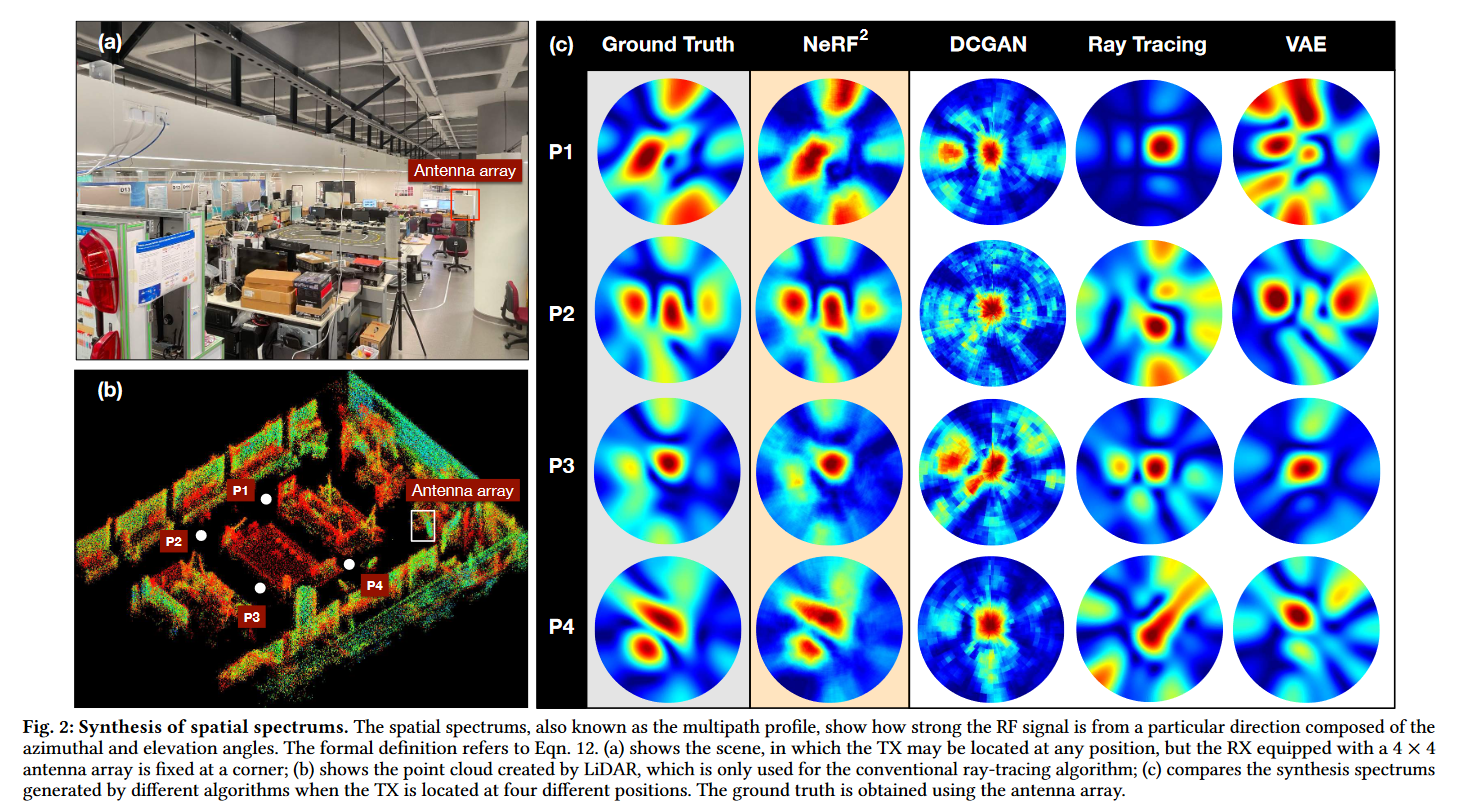
4.2 Spectrum Synthesis

  • Ground truth: Unfortunately, Fig. 2-(c) (1st column) shows possible multiple peaks because of the multipath propagations in such a complex environment.(出现多个峰的原因可能是因为复杂环境中的多径传播)

Common Criterion: structural similarity index measure(SSIM)

SSIM越高，表明这两个图像越相似。我们随机选择100个位置使用这四种算法来合成空间频谱。

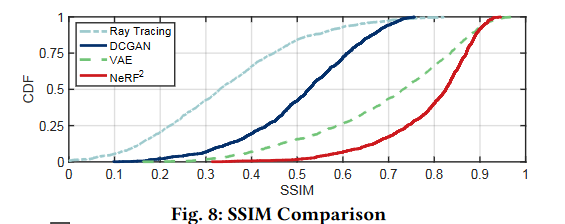
这些合成空间光谱与地面真实之间的SSIM的CDF如图8所示。特别是，RayTrking、DCGAN、VAE和NeRF2的SSIM的中位数分别为0.33、0.52、0.73和0.82，其第90个百分位数分别为0.56、0.67、0.89和0.91。

4.3 Performance of Turbo-Learning

为了量化NeRF2的好处，我们将Turbo-Learning应用到AOA估计中，目的是确定line-of-sight的方向。

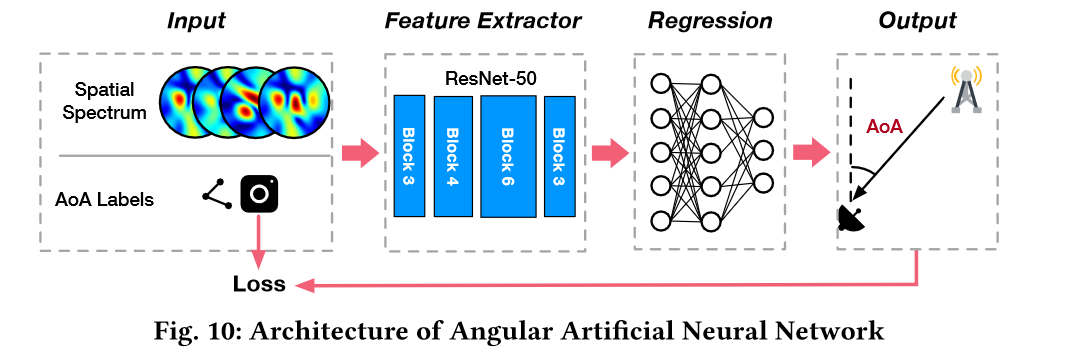
  • Naive Learning: 我们使用10%的真实训练数据集(TS，总共8K)来直接训练人工神经网络。在这种方法中，不涉及NeRF2

  • Turbo-Learning: 我们使用真实数据集的相同10%来训练NeRF2。然后，我们使用经过良好训练的NeRF2生成剩余90%的合成数据集(SS)。最后，将10%的真实数据集和90%的合成数据集(即turbocharger)混合训练神经网络。

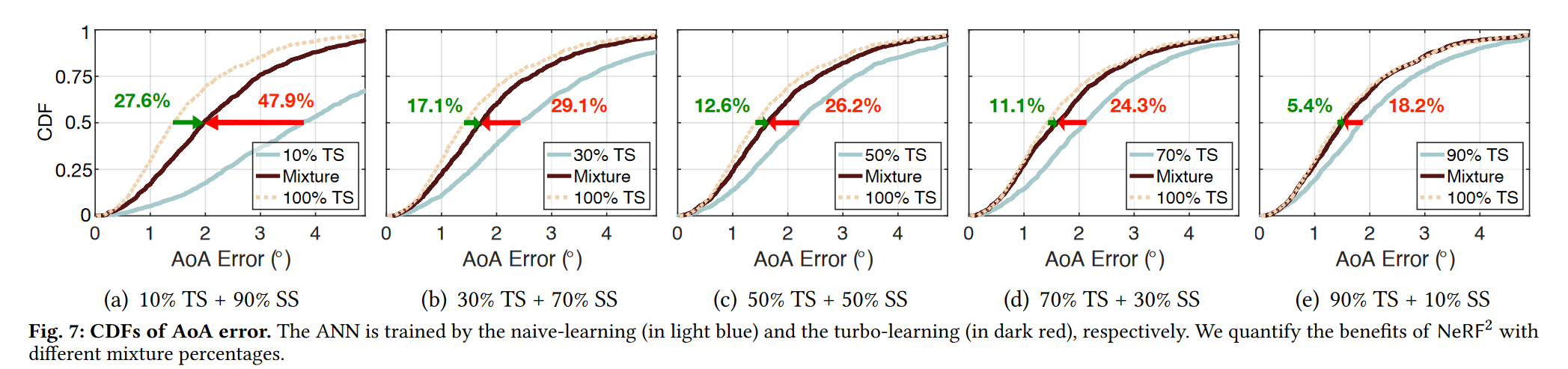
NeRF2的优势在于显著减少了真实训练集的数量和相应的工作量

4.4 Large-scale Experiments

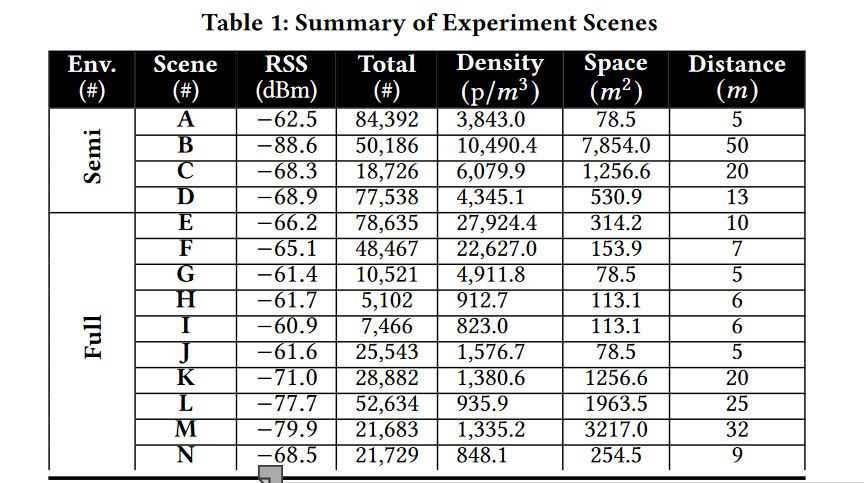
我们使用相同的天线阵列从14个场景(标记为A∼N)的531,504个位置收集了一个巨大的数据集。表1列出了这些设置。图9显示了其中八个设置(由于空间限制)。

AOA的准确性结果如图11所示。从该图中，我们有以下两个发现：

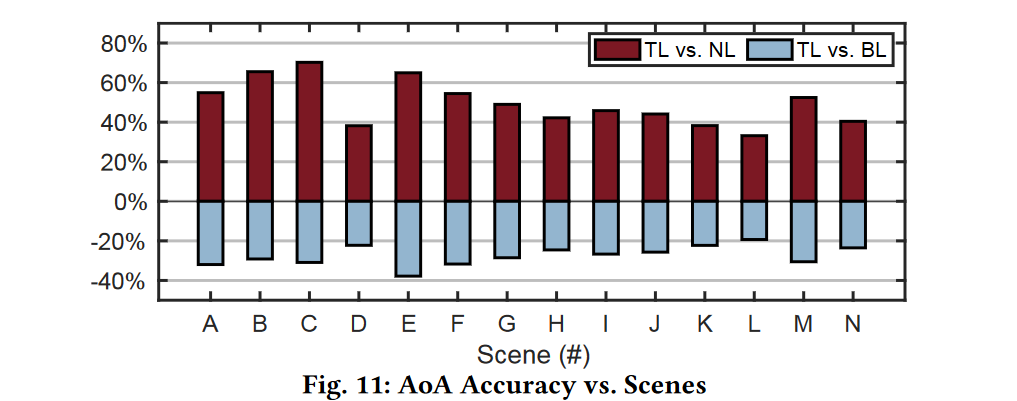
  • 与naive learning(NL)相比，turbo-learning(TL)可以提供33%-70%的改进。平均为49.5%。由此可见，涡轮学习对性能的提升是一种跨场景的普遍现象。

  • 与baseline(BL)相比，涡轮学习可以保持−27.5%的差距，其中负号表示准确率低于。然而，由于只使用了10%的训练集，Turbo学习为数据集收集节省了90%的工作量。

我们的实验揭示了影响turbo-learning性能的两个关键因素： 1. 数据集的数量: dataset 数量越多, turbo-learning 效果越差 2. 数据集的质量: 比如有人走过之类的.

5 FIELD STUDY: BLE LOCALIZATION